
Pas besoin d’être rigide – c’est en réalité une question pointue. Vous êtes-vous déjà demandé pourquoi on parle d’un « virage à 180 degrés » pour désigner un changement d’opinion radical ? Ou pourquoi une société de jeux vidéo pourrait appeler son nouveau produit « Xbox 360 » pour suggérer qu’il offre une expérience de divertissement complète ?
Comme souvent, la réponse se trouve dans les mathématiques, et plus précisément dans la géométrie. Ces deux expressions courantes font en réalité référence au nombre de degrés dans une rotation complète, ou, pour le dire plus simplement, au nombre de degrés dans un cercle entier.
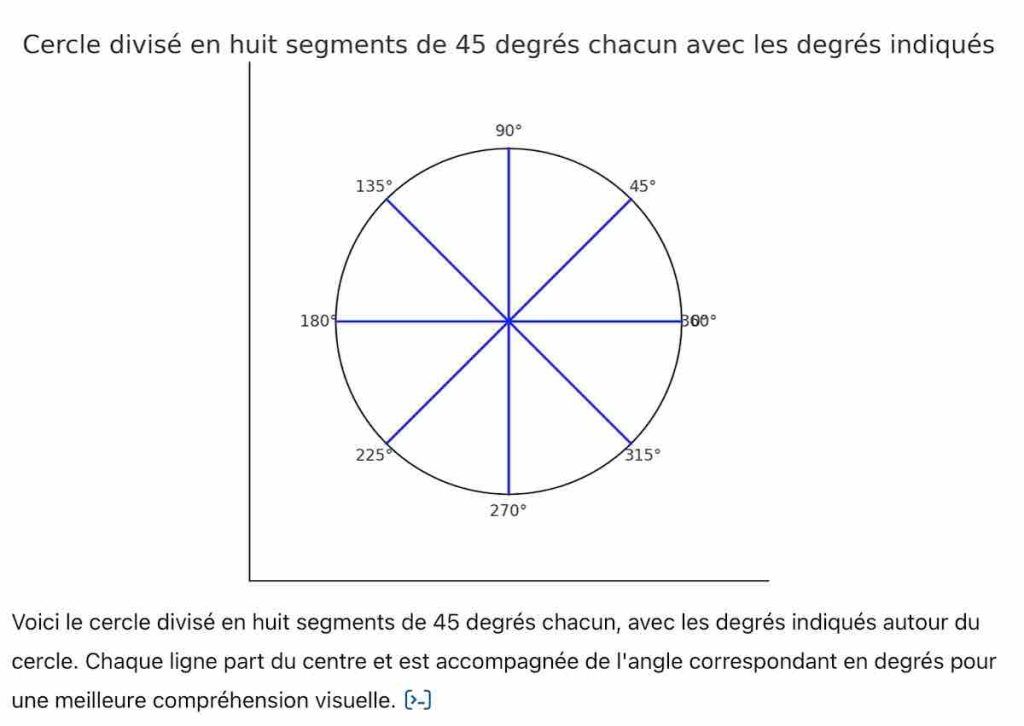
Pourquoi un cercle est-il divisé en 360 degrés ?
Vous êtes-vous déjà demandé pourquoi nous avons choisi de diviser un cercle en 360 parties égales ? Cette décision peut sembler arbitraire à première vue, surtout si vous n’êtes pas un fervent admirateur des mathématiques ou un passionné des systèmes de mesure. Alors, pourquoi 360 degrés ? Et pourquoi ce choix persiste-t-il encore aujourd’hui ?
Pour comprendre l’origine de cette division, il faut remonter à l’Antiquité, bien avant que les mathématiques ne deviennent une discipline formelle. La réponse se trouve en fait chez les Babyloniens. Il y a environ 4 500 ans, vers 2400 avant J.-C., ces anciens mathématiciens ont été parmi les premiers à diviser un cercle en 360 degrés. Alors, est-ce simplement parce que les Babyloniens l’ont décidé il y a si longtemps que cette division est restée inchangée jusqu’à nos jours ?
Bien que cette explication simple soit en partie correcte, il y a beaucoup plus à découvrir sur ce choix historique. En réalité, nous ne savons pas avec certitude ce qui a motivé les Babyloniens à choisir 360 comme nombre de degrés dans un cercle, mais plusieurs hypothèses intéressantes existent.
L’une des raisons possibles est que 360 est un nombre exceptionnellement pratique pour les calculs. En effet, 360 est un nombre hautement composite, ce qui signifie qu’il a de nombreux diviseurs. Cela le rend très utile pour les divisions en fractions simples, une caractéristique précieuse pour les anciens astronomes et géomètres.
Une autre hypothèse se base sur l’observation des cycles astronomiques. Par exemple, le nombre de jours dans une année solaire est assez proche de 360, ce qui pourrait avoir influencé cette décision. De plus, les Babyloniens utilisaient un système sexagésimal (base 60), et 360 est un multiple de 60, ce qui aurait facilité les calculs et les représentations géométriques.
Enfin, il est possible que cette division ait été choisie pour sa beauté géométrique et ses propriétés mathématiques. Le fait que 360 puisse être divisé en de nombreux sous-ensembles simples aurait pu rendre cette approche attrayante pour les savants de l’époque.
Ainsi, bien que la division d’un cercle en 360 degrés soit une tradition ancienne qui perdure, elle repose sur des principes mathématiques et astronomiques qui ont suscité l’intérêt des Babyloniens. Cette pratique a été transmise à travers les âges et a trouvé un écho dans les systèmes de mesure modernes.
Alors, la prochaine fois que vous tracez un cercle ou mesurez un angle, souvenez-vous que vous suivez une tradition millénaire fondée sur l’ingéniosité et l’observation des anciens Babyloniens !
L’Argument de la divisibilité : L’influence du système sexagésimal Babylonien

L’incroyable sophistication astronomique des Babyloniens était le fruit de leur profonde obsession pour la mesure du ciel, une obsession qui surpassait celle de toutes les autres civilisations contemporaines et même de nombreuses sociétés ultérieures. En fait, jusqu’au XVIe siècle, les astronomes occidentaux utilisaient des méthodes d’observation et d’enregistrement des mouvements planétaires remarquablement similaires à celles développées par les Babyloniens trois millénaires plus tôt.
Pourquoi cette continuité des techniques astronomiques ? La réponse réside en grande partie dans un aspect fondamental des mathématiques babyloniennes : leur système de comptage. Contrairement à notre système numérique moderne, qui est basé sur la base 10, les Babyloniens utilisaient un système sexagésimal, c’est-à-dire un système en base 60.
Ce choix du système sexagésimal n’était pas anodin. Le système sexagésimal offrait des avantages considérables en termes de divisibilité, ce qui était crucial pour les calculs astronomiques. En effet, 60 est un nombre exceptionnellement pratique, car il possède de nombreux diviseurs : 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 et 60. Cette richesse en diviseurs permettait aux Babyloniens de réaliser des fractions simples et précises, essentielles pour leurs observations du ciel et leurs calculs astronomiques.
Ainsi, la capacité de diviser un cercle en 360 degrés est directement liée à ce système sexagésimal. Le nombre 360 est un multiple de 60, et il s’adapte parfaitement à la logique de leur système de mesure. En divisant le cercle en 360 degrés, les Babyloniens pouvaient utiliser leur système sexagésimal pour effectuer des calculs avec une grande précision, reflétant ainsi leur sophistication en astronomie.
Ce système sexagésimal a donc joué un rôle clé dans le développement des techniques astronomiques babyloniennes, et son influence a perduré bien au-delà de leur époque, façonnant la manière dont les astronomes ont observé et enregistré les mouvements célestes pendant des siècles.

Pourquoi 360 Degrés ? L’Argument de la Divisibilité
L’idée que les Babyloniens aient choisi de diviser un cercle en 360 degrés n’est pas aussi arbitraire qu’il pourrait y paraître. Comme l’explique Chris Linton, professeur de mathématiques appliquées à l’Université de Loughborough dans son livre From Eudoxus to Einstein: A History of Mathematical Astronomy, « la raison pour laquelle 60 a été utilisé n’est pas entièrement claire, mais il est probable que ce choix découle du fait que 60 est divisible par de nombreux petits nombres entiers, ce qui facilite les calculs sans avoir besoin de fractions. »
Cette propriété était un avantage majeur dans le contexte des mathématiques pré-Zénoniennes. Comparons le nombre 60 au nombre 10, par exemple : alors que 60 peut être divisé par 3 et donner un nombre entier (20), ce n’est pas le cas pour 10 ; de même, 10 ne peut pas être divisé par 4 ou 6 sans obtenir une fraction. En revanche, pour les Babyloniens, ces divisions étaient simples grâce à leur système sexagésimal.
Mais le choix du nombre 360, qui est 60 multiplié par 6, présente des avantages encore plus marqués. En effet, 360 est ce qu’on appelle un « nombre hautement composé supérieur », un terme moderne qui décrit un nombre ayant une grande quantité de diviseurs. Le nombre 360 peut être divisé de manière entière par 24 diviseurs différents : 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180, et 360. Cette multitude de diviseurs rend le calcul et les divisions particulièrement simples.
Prenons un exemple pour mieux comprendre. Si vous deviez diviser le monde en 24 fuseaux horaires en utilisant un système basé sur 100 degrés par révolution, vous auriez à mesurer des angles récurrents de 4,166666… degrés, ce qui est peu pratique pour un cartographe et quasiment impossible pour un mathématicien. En revanche, en utilisant 360 degrés, chaque fuseau horaire correspond parfaitement à un angle de 15 degrés, rendant la tâche beaucoup plus simple.
Ce choix du nombre 360 peut également être lié à la manière dont les mathématiciens grecs ont hérité des traditions babyloniennes. Les premiers géomètres grecs avaient une grande affinité pour les triangles et la symétrie. Par exemple, en traçant un cercle et en y dessinant un triangle équilatéral (avec trois rayons partant du centre et reliant leurs extrémités), vous créez un triangle dont chaque angle mesure 60 degrés. Cette relation entre le cercle et le triangle équilatéral, avec des angles de 60 degrés, peut avoir contribué à la persistance de l’idée de diviser le cercle en 360 degrés.
L’utilisation du nombre 60 pour les calculs et la multiplication par 6 pour obtenir 360 sont des choix pratiques enracinés dans la géométrie et la symétrie qui ont perduré à travers les âges.
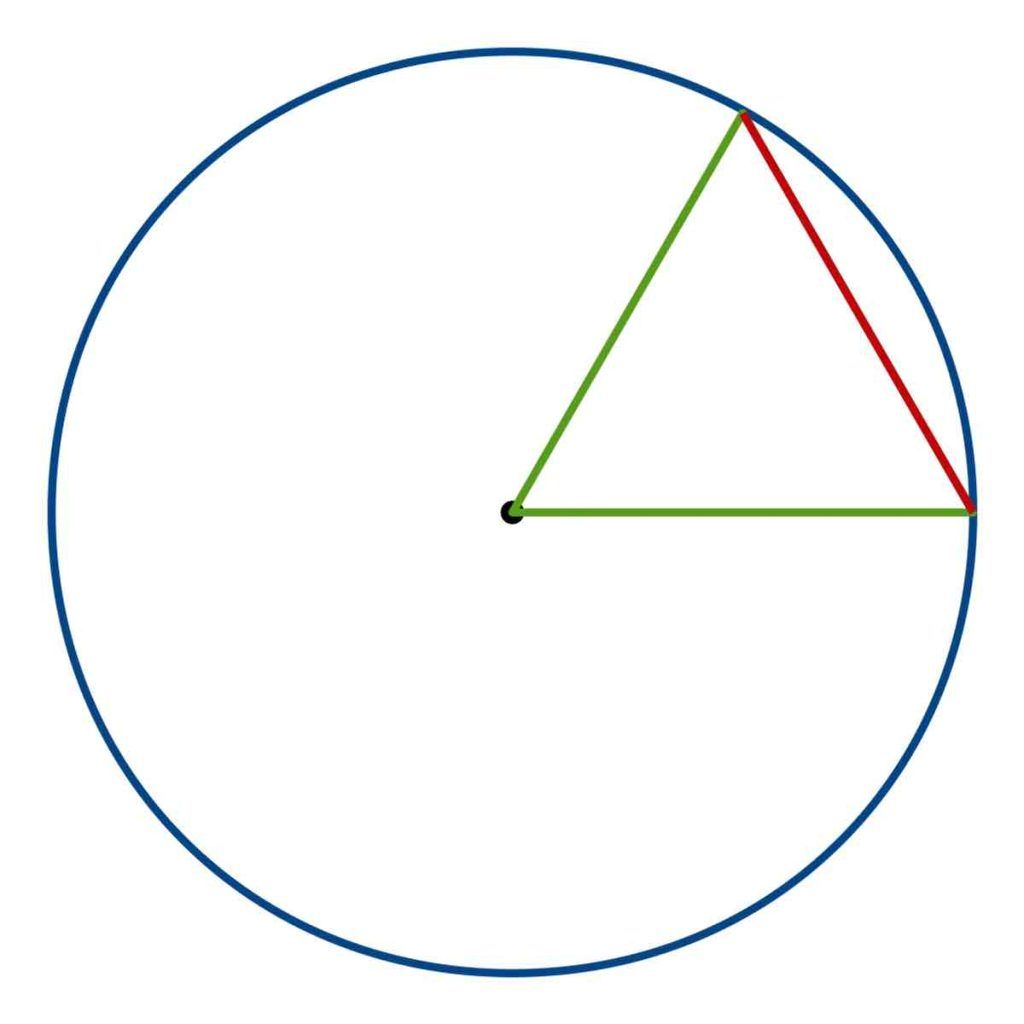
Assemblez six de ces triangles et ils couvriront tout le cercle, faisant de cette configuration six fois 60 une base naturelle pour l’ensemble du monde de la géométrie.
Une unité de base encore plus farfelue : Les radians
En mathématiques, la complexité ne connaît pas de limites, et il est toujours possible de concevoir des systèmes de mesure encore plus compliqués que ceux que nous utilisons au quotidien. C’est le cas du radian, une unité de mesure des angles qui, bien qu’adoptée depuis longtemps dans les cercles scientifiques, est bien plus complexe que les degrés.
Bien que le concept de radian soit connu des mathématiciens musulmans depuis au moins le 15e siècle, il n’a été formalisé en tant qu’unité mathématique qu’au 18e siècle. Aujourd’hui, le radian est la norme dans des domaines plus avancés que la simple géométrie, et pour une bonne raison : il offre une manière plus naturelle de mesurer les angles, avec des formulations de résultats plus élégantes et une simplification des calculs qui peuvent devenir étranges et complexes si l’on utilise des degrés.
Mais, du point de vue de quelqu’un qui n’est pas habitué à ces notions, les radians peuvent sembler encore plus compliqués que les degrés. Pourquoi ? Parce que dans le système radian, un cercle complet est mesuré en… 2π radians.
Oui, c’est bien ce π – le célèbre nombre irrationnel et transcendantal que l’on ne peut exprimer exactement avec des chiffres réels. Alors, la prochaine fois que vous vous sentez frustré par le fait de devoir travailler avec les 360 degrés d’un cercle pour vos devoirs de géométrie, souvenez-vous que cela pourrait être bien pire !
En effet, si nous devions nous souvenir que les angles internes d’un triangle équilatéral sont chacun de 1,0471975511965977461542144610931676280657231331250352736583148641 radians, vous pouvez imaginer à quel point cela serait plus difficile !
Les radians, malgré leur complexité apparente, offrent une approche mathématique plus élégante et plus efficace pour les calculs complexes, mais les degrés restent une unité plus intuitive pour les situations quotidiennes. Ainsi, la prochaine fois que vous vous sentez perdu avec les 360 degrés d’un cercle, rappelez-vous qu’il y a toujours des systèmes de mesure encore plus étranges et difficiles à appréhender, comme celui des radians.

